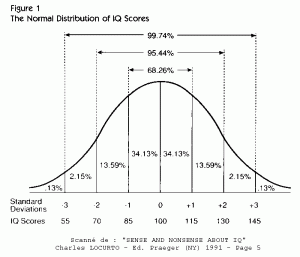
En normalisant les tests de QI avec un écart-type de 15 et une moyenne de 100, David Wechsler (1939) a permis à la fois leur application aux adultes, et une estimation directe du nombre de personnes concernées par chaque niveau. Le problème est que cette estimation n’est valide qu’aux alentours de la moyenne : l’effet de tassement1 provoqué par ce mode de calcul mène à des estimations très largement inférieures à la réalité pour les hauts QI. En conséquence, hormis pour les QI très proches de la moyenne, il est impossible de traduire directement un QI Wechsler en un QI en âge mental. Dans le Guide Pratique de l’Enfant Surdoué2 Jean-Charles Terrassier donne l’exemple d’une fillette de 6 ans ayant un QI standard de 149 et un QI en âge mental de 179 !
Peu de solutions ont été proposées pour résoudre ce problème de décalage entre les deux types de QI. Dans un article très intéressant, Bob Seitz de la Mégafoundation3 propose, à la suite de Geoffrey Thomas Sare (1951) et du Dr. Robert Dick (2000) de remplacer le QI par le Ln-QI. L’idée est que si le QI en âge mental ne suit pas une loi normale, le logarithme naturel (LN) de ce QI est parfaitement représenté par la loi Normale. Le calcul indiqué est : un ratio d’âge mental de 1,4 (correspondant à un QI classique de 140) a pour logarithme naturel 0,3365, auquel il suffit de rajouter 100 pour obtenir un résultat de 133,65. Et, selon l’auteur, la distribution de ces résultats, tout au long du QI, correspond bien à une loi normale de moyenne 100 et d’écart-type 15. Dès lors, la simple application de cette formule permet d’avoir une estimation plus précise, délivrée de l’effet de tassement, du nombre de personnes concernées par chaque niveau de QI : c’est ce que j’ai fait pour le site Douance4.
Faut-il donc abandonner le QI pour le remplacer par le LN-QI ?
Le LN-QI semble donc un très bon candidat pour remplacer, avantageusement, le QI. Il serait beaucoup plus facile pour chacun de lire sur une table, comme celle du site Douance, la correspondance entre le QI Classique et le LN-QI, que de recalculer un QI classique à partir de chaque résultat à chaque subtest. Hélas, tout n’est pas si rose.
Tout d’abord, la formule employée par Bob Seitz perd toute validité pour les QI inférieurs à 100 (par exemple, LN-QI (36) = – 2,17). C’est une première restriction importante à son utilisation, même si peut-être des mathématiciens pourront trouver une solution à ce problème5.
Ensuite, si l’on reprend l’exemple de Jean-Charles Terrassier cité plus haut, on s’aperçoit que le LN-QI ne donne pas les mêmes résultats que les QI standards : pour un QI classique de 179, le LN-QI est de 158, pas de 149 comme trouvé par Terrassier. En d’autres termes, l’utilisation du LN-QI ne résoud pas, au moins dans ce cas, le problème initial. D’ailleurs, Bob Seitz a trouvé que le LN-QI ne correspond aux données Terman que pour les QI supérieurs ou égaux à 165.
A la fin de sont article, daté de novembre 2002, Bob Seitz indique : To be continued. Il reste en effet des améliorations à effectuer pour que cette méthode puisse être généralisée. On retiendra cependant le principe général, c’est-à-dire que si le QI classique ne correspond pas à une courbe en cloche, son logarithme naturel en est beaucoup plus proche, au moins pour les très hauts QI, qui sont bien beaucoup plus nombreux que ne le laisse penser le QI standard.
Historique des modifications
| Date | Historique |
|---|---|
| 10 mars 2024 | Mise à Jour liens |
| 30 Octobre 2003 | 1ère Mise en ligne |
Notes :
-
Voir la FAQ QI du site Douance.org ↩
-
Guide Pratique de l’Enfant Surdoué – Terrassier – Gouillou – ESF REED – 6ème édition 2003 ↩
-
Seitz, R. N. (2002). Are IQ Distributions Ln-Normal Rather Than Gaussian? Megafoundation. 6 Septembre 2002. ↩
-
On ne peut utiliser la symétrie de la courbe, puisque celle-ci n’est plus valide aux extrémités : il existe des QI classiques supérieurs à 200, mais il n’en existe pas d’inférieurs à 0. ↩